Temperature Field Calculated From Equation 3-5

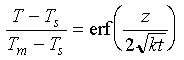
First some notes on the error function, erf.

To illustrate the temperature field, we adopt T=1400 °C. For depth we will work in units of km, and for time in units of My so that the appropriate thermal diffusivity is 25 (km)/(My). We will build a grid for 0 to 100 km depth and 0 to 100 My of crustal age in steps of 5 km and 5 My respectively. The solution at t=0 has to be taken directly from equation 3-2 because of the singularity at t=0 in equation 3-5. The calculations are done with the MATLAB script, /usra/mcduff/oc501/plate.m:

kappa=25;
Tmelt=1400;
z=0:5:100;
t=0:5:100;
for I=1:1:21
T(I,1)=Tmelt;
for J=2:1:21
T(I,J)=Tmelt*erf(z(I)/(2*sqrt(kappa*t(J))));
end
end
cs=contour(t,-z,T);
clabel(cs)

If we think of the base of the lithosphere as corresponding to a particular isotherm, say the 1200 °C isotherm, we can trace the growing thickness of the lithosphere as the crust ages. However, because of the semi-infinite geometry adopted, it grows to an unreasonable large thickness, as compared to the constraints provided by seismic studies of the oceanic lithosphere. The temperature gradient (and the conductive heat flux) decreases, most rapidly at first and then more slowly.