Sediment transport is expressed in terms of a flux of material through a plane surface perpendicular to the flow (dimensions M L-2 T-1):
FIGURE
Restricting attention on the two dimensional case, the transport can be integrated vertically:
![]()
The quantity q has the dimensions M L-1 T-1 so that one would obtain the transport within a channel in terms of mass per time by multiplying by the channel width.
Ultimately the interest in evaluating sediment transport is to assess the effects of transport on erosion or deposition of the bed:
FIGURE
Let the porosity, p, be the volume percent of the bed that is fluid. In the absence of a vertical sediment flux the depth of the bed relative to some datum will be related to the downstream change in sediment transport:
![]()
When dq/dx is positive, material is progressively being added to the transported load and h at a point increases with time (i.e., material is eroded).(Note: this equation needs to be fixed should be 1/rho)
Bedload and suspended load are distinguished by the dominant forces acting on the particles being transported. Bedload transport is dominated by a balance of applied stress acting to put particles into motion and gravitational forces acting to keep them in place. Suspended load is dominated by a balance of turbulent forces acting to keep particles in suspension and gravitational settling. Besides this separation by physical mechanisms involved, the two modes of transport are also distinguished by being measured with quite different techniques.
Bedload Transport
The physics of bedload transport involve many complicated mechanisms and feedbacks and so becomes difficult to express in simple terms. Many equations for bedload include empirically derived terms which may or may not be of general utility. Historically three approaches have been taken in developing expressions for the bedload:
shear stress relationships (DuBoys approach)
force balances (Einstein, Bagnold approaches)
discharge relationships (Schoklitsch approach)
The last of these three is relevant to analysis of channels and is not considered here. The first two will ultimately yield expressions that may be comparable, but the starting point is quite different.
DuBoys approach posits that the sediment transport is a function of the boundary stress. As one example, assume that this function can be represented by the power series:
![]()
When there is no stress, there is no transport and so k1 must be zero. Just at the critical condition q is zero as well:
![]()
Thus
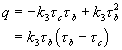
The characteristic constant is then determined empirically. Variants exist parameterizing sediment transport with similar functions, e.g.,
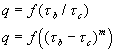
While effective in parameterizing transport, the physical basis for this class of equations is not always obvious and it would be preferable to begin with some consideration of the forces that are acting. The approach of Bagnold is the one most commonly applied in the marine environment. Bagnold posits that the transport q, as measured by the weight of particles being transported should reflect the power expened per area of bed in order to initiate transport.
Recall that the work is the integral of a force acting over some distance and the power is the work accomplished over some time. On a per area basis then, the dimensions of force are ML-1T-2, of work MT-2 and of power MT-3.
Applying these ideas:
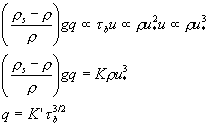
The dimensionless constant K can be loosely thought of as an efficiency of transport, i.e., what fraction of the work is going to motion of sediment. (Loosely because in some situations K will exceed one somewhat.)
In this form we see an immediate problem. The transport does not approach zero at the critical stress. This has been solved in two ways (empiricism returns), either through the parameterization of K or through introducing a modified term in the stress related term. Some examples:
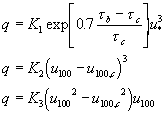
| Oceanography 540 Pages Pages Maintained by Russ McDuff (mcduff@ocean.washington.edu) Copyright (©) 1994-2001 Russell E. McDuff and G. Ross Heath; Copyright Notice Content Last Modified 3/2/2001 | Page Last Built 3/2/2001 |