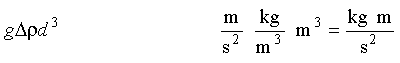
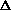 Th.
Consider
a parcel of fluid of scale d (d x d x d) located between these plates.
Th.
Consider
a parcel of fluid of scale d (d x d x d) located between these plates.
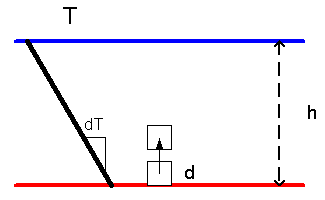
Figure 10-3
Eq 10-2:![]()
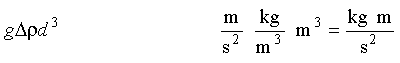
where g is gravitational acceleration and ![]() is density.
Further suppose that this density contrast is solely due
to a contrast between its temperature and the surroundings:
is density.
Further suppose that this density contrast is solely due
to a contrast between its temperature and the surroundings:
Eq 10-3:![]()
![]()
where ![]() is the thermal expansion coefficient and T is
temperature.
Because the parcel is less dense than its surroundings, it will tend to move upwards.
A viscous force:
is the thermal expansion coefficient and T is
temperature.
Because the parcel is less dense than its surroundings, it will tend to move upwards.
A viscous force:
Eq 10-4:![]()
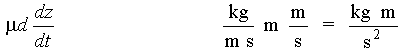
will act against the buoyancy force. In this expression µ is viscosity, z is the vertical spatial coordinate, and t is time. When these two forces balance:
Eq 10-5:![]()
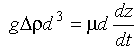
In addition, the parcel will be losing heat to its new surroundings by conduction, thereby reducing its temperature. The rate at which heat is lost will be proportional to the surface area of the parcel. Thus temperature (and so the density term) is a function of time:
Eq 10-6:![]()
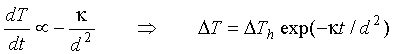
where ![]() is the thermal conductivity.
Combining 10-3, 10-5 and 10-6 and rearranging:
is the thermal conductivity.
Combining 10-3, 10-5 and 10-6 and rearranging:
Eq 10-7:![]()
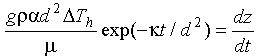
How far can the parcel move in infinite time? We integrate from zero to infinity:
Eq 10-8:![]()
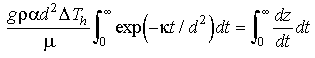
to find that the distance traversed, z, is:
Eq 10-9:![]()
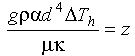
The terms in the numerator of equation 10-9 have their origin in the buoyancy force and promote upward motion while increasing either viscosity or thermal conductivity in the denominator limits upward motion.
To be able to convect heat, there must be movement across the distance between the two plates separated by a distance h in finite time and so:
Eq 10-10:![]()
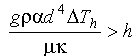
By scaling the fluid parcel to the plate separation, through an arbitrary factor f:
Eq 10-11:![]()
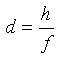
substituting into equation 10-10 and rearranging it follows that:
Eq 10-12:![]()
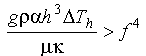
The left hand side of equation 10-12 is called the Rayleigh number:
Eq 10-13:![]()
![]()
Lord Rayleigh showed through linear perturbation analysis (for a general
discussion see (13), section 7.1.2 or the derivation
in (11), section 6-18),
that for
thermal instabilities to grow in a fluid, the Rayleigh number would have
to exceed a critical value (the f![]() scale on the right hand side). When:
scale on the right hand side). When:
Eq 10-14:![]()
![]()
the temperature profiles between the two plates will be conductive, while when:
Eq 10-15:![]()
![]()
a cellular convection will be established, driving the isotherms upwards in the zone of rising fluid and downwards in the zone of downwelling. The value of the critical Rayleigh number depends on the particular geometry and boundary conditions. For relevant geometries it lies between 657 (free boundaries) and 1708 (rigid boundaries).
Will fluids in the ocean crust convect? Consider a open fracture penetrating to great depth, say a kilometer. The Rayleigh number is:
Eq 10-16:![]()
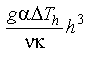
(Here the viscosity and density term have been replaced with the kinematic viscosity.). For some representative values
![Table]](f2-19.gif) (Table VII-1)
(Table VII-1)
the Rayleigh number is about 10![]()
![]() --far in excess of the critical value.
--far in excess of the critical value.
| Oceanography 540 Pages Pages Maintained by Russ McDuff (mcduff@ocean.washington.edu) Copyright (©) 1994-2002 Russell E. McDuff and G. Ross Heath; Copyright Notice Content Last Modified 1/17/2002 | Page Last Built 1/17/2002 |