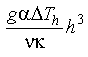
Eq 10-1:![]()
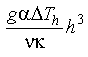
Horton and Rogers and later Lapwood extended this analysis to a situation where a porous medium fills the space between two horizontal plates separated by a distance h. (Details of the analysis can be found in (14), section 5.1, or (11), section 9-9.) Horton shows that the criterion for establishing convection in the porous medium, i.e., the onset of Rayleigh-Darcy instabilities is:
Eq 10-3:![]()
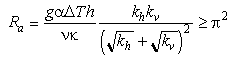
For values representive of newly formed oceanic crust (a 6 km crust with a temperature gradient of 1200°) the critical Rayleigh number is exceeded:
Eq 10-4:![]()
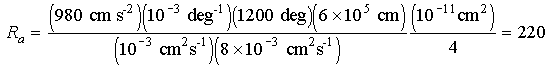
The length scales, l, for the convection cells scale with the permeability:
Eq 10-5:![]()
![]()
In isotropic media, the horizontal spacing of cells should be similar to the depth of penetration of the fluid; spacing of vent systems along the ridge axis carries information on the depth to which fluid circulates.
Darcy flow can be used as a starting point to model the convection of fluid through the oceanic crust. In three dimensions:
Darcy's Law
Eq 10-6:![]()
![]()
conservation of fluid
Eq 10-7:![]()
![]()
conservation of heat
Eq 10-8:![]()
![]()
In these equations q is the mass flux of fluid, k is the permeability,
![]() is the kinematic viscosity, P is pressure,
is the kinematic viscosity, P is pressure, ![]() is density, g is gravitational
acceleration, Cp is the heat capacity with the additional subscript m
denoting the porous medium (solid and fluid) and the subscript f denoting the fluid filling the
pores,
is density, g is gravitational
acceleration, Cp is the heat capacity with the additional subscript m
denoting the porous medium (solid and fluid) and the subscript f denoting the fluid filling the
pores, ![]() is the thermal conductivity (note non-standard use of kappa), and u is the spreading velocity. In the
energy balance, the three terms on the right hand side of the equation
represent repectively the
is the thermal conductivity (note non-standard use of kappa), and u is the spreading velocity. In the
energy balance, the three terms on the right hand side of the equation
represent repectively the
The system of equations is generally solved numerically. The methodology is to introduce stream functions, i.e., contours of constant q, and cast the equations as finite differences in order to obtain a solution.
One of the first applications of this approach can be found in (15). The boundary conditions for flux of mass are a free upper boundary and impermeable sides and bottom. The initial condition for temperature is taken as the conductive temperature distribution. The boundary conditions for temperature are a horizontal flux condition at axis which matches the heat content of the injected molten material and the conductive heat flux at bottom boundary.
The model is applied in the context of a heat flow survey on the flanks of Galapagos Rift conducted in 1976-77. For a mid-ocean ridge this is in an unusual setting in that it is near to the equator where the sedimentation rate is high, about 50 m/My. Because of the high sedimentation rate, conductive heat flow is measurable on crust as young as 100,000 y. There is virtually a total sediment blanket within the 1 My isochron. Data from the heat flow survey are shown here:
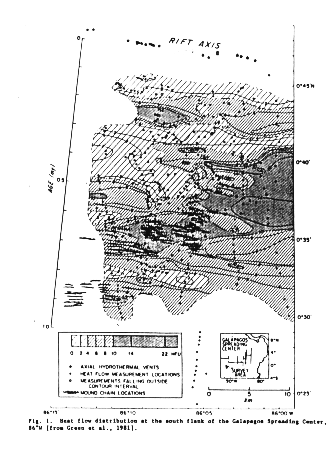
Figure 10-1
The cases shown are for varying depths of fluid penetration. All have exponentially decreasing permeability with depth though the value at upper surface is varied:
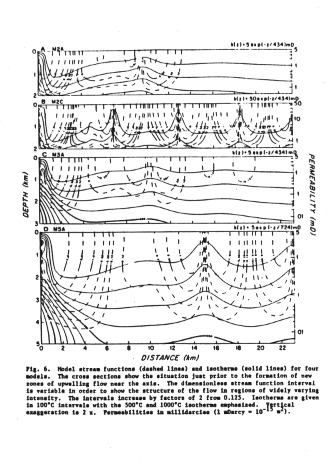
Figure 10-2.
The modeling approach was to find the combination of parameters that best matched the conductive heat flow distribution in terms of the measured conductive heat flow and the geometry of the convection cells. The data:
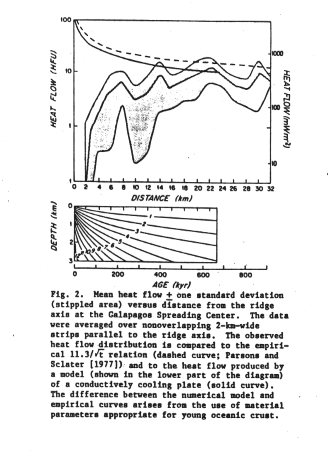
Figure 10-3
The models:
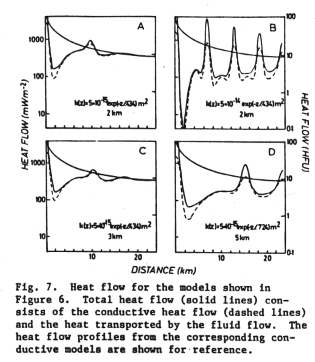
Figure 10-4
Data averaging prevents finding an exact match.
For
models with a reasonable match to the observations, the fluid output is about 5 x 10![]() g
of water per year per cm of ridge which translates to 2 x 10
g
of water per year per cm of ridge which translates to 2 x 10![]() cal/km of ridge/y, much
smaller than reference value calculated earlier when discussing local scales, 5
x 10
cal/km of ridge/y, much
smaller than reference value calculated earlier when discussing local scales, 5
x 10![]() . There are two possible
reasons
for this discrepancy: the slower spreading (factor of 3.5/5) and
the possibility that the insulating effect of having a sediment cover impedes convection. Cooling of the upper
crust increases shallow temperature gradients and thus the conducted heat flux from
below:
. There are two possible
reasons
for this discrepancy: the slower spreading (factor of 3.5/5) and
the possibility that the insulating effect of having a sediment cover impedes convection. Cooling of the upper
crust increases shallow temperature gradients and thus the conducted heat flux from
below:
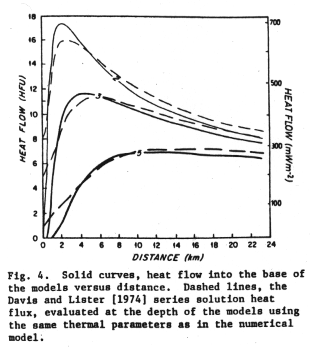
Figure 10-5
The cell geometry appears to be stable despite advection of the plate away from the axis, however this may be an artifact of the impermeable off-axis boundary condition:
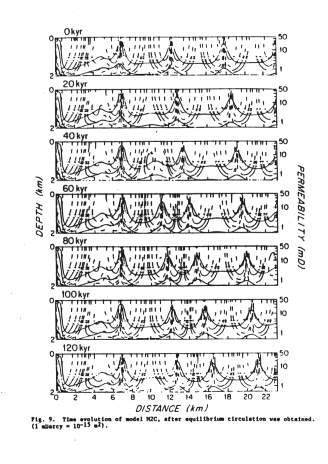
Figure 10-6
A final observation is the correspondence of the
depth of penetration of the most vigorous streamlines and the 300-400°C
isotherms. The origin of this behavior is in the dependence of the Rayleigh number
on ![]() and
and ![]() . As a function of temperature, the expansion coefficient
shows a strong maximum in this temperature range (near to the critical point)
and the viscosity a minimum
thereby promoting convection:
. As a function of temperature, the expansion coefficient
shows a strong maximum in this temperature range (near to the critical point)
and the viscosity a minimum
thereby promoting convection:
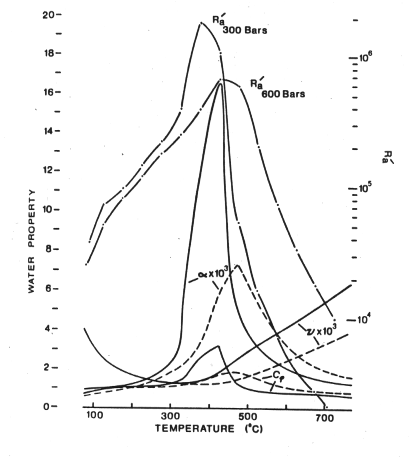
Figure 10-7
| Oceanography 540 Pages Pages Maintained by Russ McDuff (mcduff@ocean.washington.edu) Copyright (©) 1994-2002 Russell E. McDuff and G. Ross Heath; Copyright Notice Content Last Modified 10/21/2002 | Page Last Built 10/21/2002 |