Ocean 540
Winter 2001
Problem Set #3

Due Friday, February 23, 2001

1. If the global convective heat flux at the mid-ocean ridge is 2.5x10¹⁹ cal/y and the fluids discharge at 400°C, what is the characteristic time for passage of the volume of the ocean through newly formed oceanic crust? through hydrothermal plumes? Munk's abyssal recipe calls for generalized upwelling of ~4 m/y. Suppose the 1x10¹⁹ cal/y of the global ridge convective heat flux discharges in the South Pacific (area 89x10⁶ km²). Compare the integrated vertical transport in the South Pacific due to rising hydrothermal plumes and generalized upwelling.
2. Figure 2 in Lecture 19 shows the present day distribution of ¹⁸O in the ocean. What would this same graph look like in glacial times if the mean ocean was enriched in ¹⁸O by +1.5‰ and there was no production of deep water in the North Atlantic. Explain how you have determined the position of each of the major features in your graph. What does this result imply for the expected shift in ¹⁸O measured in benthic forams sampled in the North Atlantic? the South Atlantic? the Pacific Ocean?
3. The Imbrie et al. model of radiative forcing and climatic responses emphasize the response of systems characterized by two time scales: a lag (delay) time and a response time, so that relative to the forcing we can sketch the response:

   

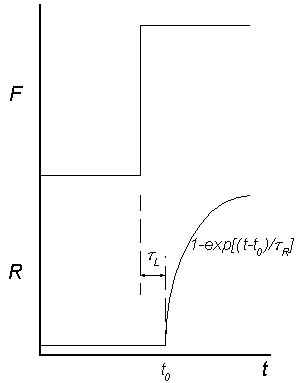
   1. Confirm that the response depicted follows from the governing differential equation:

      
      
      

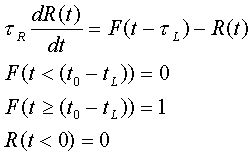
   2. The Imbrie et al. model itself involves periodic forcing. For simplicity, assume that there is no delay to the response, but the system does have a characteristic response time. Thus the governing differential equation for the responding system is:
      

      
      
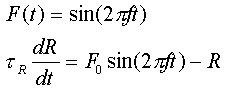
      Solve this equation for appropriate boundary conditions. Convince yourself that this system responds in an analogous fashion to the sediment bioturbation model we examined in Lecture 12.

   3. Consider forcing in the (23 ky)^-1 frequency band. What is the maximum amplitude of the response if the system responds with characteristic times of 2 and 20 ky.
   4. What does this result imply for the ability of high frequency forcing to influence different parts of the global climate system (e.g. oceans, ice caps?)
4. Note:
   The file set3-3.mat (to retrieve this "right click" on the link as "Save Link As" (Netscape) or "Save Target As" (IE)) contains values for seven variables t, R1, R2, z1, core1, z2 and core2.
   1. The records R1 and R2 are records of a hypothetical tracer measured two places at the corresponding times t at two different places in the ocean. Compute the power spectrum of the two records and identify the periodic components present in the them. Extract these frequency band and estimate the phase lag between R1 and R2, expressed as a phase angle at each frequency and as an absolute time interval.
   2. Two box cores were taken at these same two places and sectioned at two centimeter intervals. The depths and tracer measurements are given in z1 and core1 and z2 and core2 respectively. Compute the power spectrum for each core (using depth as a proxy for time). Estimate the sedimentation rates at the two sites.
   3. Extract the higher frequency record from the two cores (use filtfilt to preserve the phase information) and compare the phase and amplitude to the tracer records R1 and R2. How do you explain the differences found?
5. Assume that amorphous silica dissolution is governed by the steady-state mass balance:

   

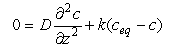
   If k is 3x10 s, D is 5x10 cms and c is 300 µM, assess the dependence of the preservation of amorphous silica on the rain rate of amorphous silica (from 1 to 10 g /cm/ky) and the bottom water concentration of dissolved silica (50 to 200 µM ).