Ocean 540: Transport Equations for Solutes in Pore Fluids

Oceanography 540--Marine Geological Processes--Winter Quarter 2000

Transport Equations for Solutes in Pore Fluids

The diffusive flux of a solute is defined by Fick's Law, a empirical expression relating the flux of material across a plane to the gradient of concentration perpendicular to that plane:

(1)

where

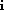F is the diffusive flux of component i (M L 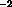T)
c is the concentration of component i (M L)
D is the diffusion coefficient of component i (L T)
x is position (L)

The sediment-water interface is usually adopted as the datum for the coordinate system, and so position x=0 moves with time. This imparts a pseudo-advection of fluid at the sedimentation rate, s. In addition, there will be upward movement of fluid relative to the solid matrix due to compaction. However in the deep sea, these terms are much smaller than the diffusive flux and can be neglected.

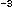The diffusion coefficient of a solute depends on the solute, the temperature and the ionic environment. Some typical values of the tracer (i.e., no ion-ion interactions) at 5°C:

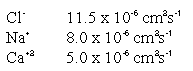
table of diffusion coefficients

The diffusion coefficient is sensitive to temperature, approximately doubling from 0 to 25°C. Within a porous medium, the additional path length to travel around particles causes the diffusion coefficient to decrease. This excess path length is expressed as a tortuosity:

(2)

where dl is the mean length of the path followed to travel a linear distance dx. The sediment diffusion coefficient, Ds, is then:

(3)

There are a number of empirical laws relating tortuosity to porosity. A reasonable approximation for deep-sea sediments is to take

(4)

The mass balance within a small volume reflects the fluxes in and out of that volume and the internal change of the pore water concentration due to chemical reaction, J:

(5)

(6)

For more information consult reference (21).

Lecture Index | Search the Ocean 540 Pages | Ocean 540 Home

Oceanography 540 Pages
Pages Maintained by Russ McDuff (mcduff@ocean.washington.edu)
Copyright (©) 1994-2000 Russell E. McDuff and G. Ross Heath; Copyright Notice
Content Last Modified 2/6/2000 | Page Last Built 2/6/2000