Physical and Geological Perspective
Sediment transport in the marine environment is driven by fluid motion. Some important transport mechanisms are depicted in Figure 1 in the context of the continental shelf:
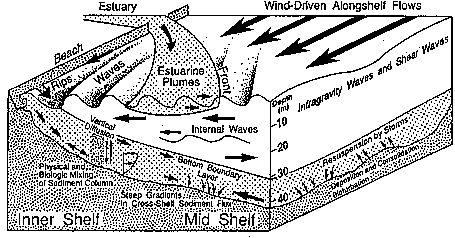 Figure 34-1
Figure 34-1Different regimes exist across the continental shelf:
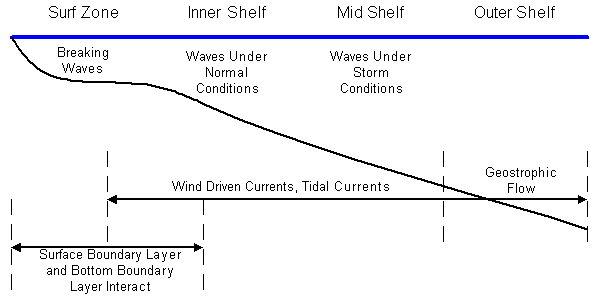
Figure 34-2
Context for Study of Boundary Layers
A boundary layer exhibits a velocity profile connecting a background oceanographic flow and a no-slip, zero velocity condition at a solid boundary.
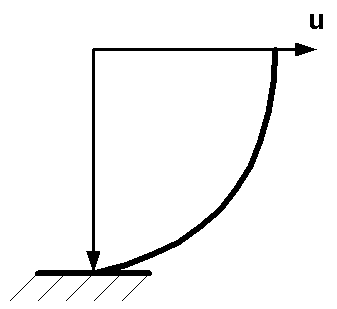
Figure 34-3
Transfer of momentum toward the boundary imposes a shear stress; when it is sufficient (i.e., exceeds a critical value), it can cause transport of sediment either as bedload or suspended load.
We begin by considering how a moving fluid interacts with a solid boundary and the nature of the velocity profile.
Shear Stress
Stress, denoted t, is a force applied to a plane surface per unit area. Dimensionally:
Eq 34-1![]()
![]()
Consider a volume element. Each of the three surfaces can have three forces acting on it, so there are nine components in all. They are denoted ![]() where the i subscript describes the surface (e.g., z would indicate the surface perpendicular to the z-axis) and the j subscript describes the direction of the force (e.g., x would indicate the force acting in the direction of the x-axis).
where the i subscript describes the surface (e.g., z would indicate the surface perpendicular to the z-axis) and the j subscript describes the direction of the force (e.g., x would indicate the force acting in the direction of the x-axis).
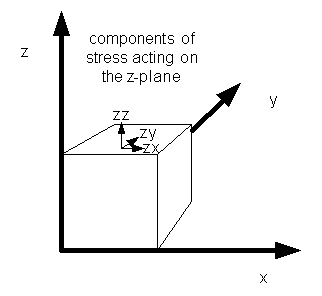
Figure 34-4
Eq 34-2![]()
![]()
Of the remaining six components, we are interested in the two acting in the x and y directions on the plane perpendicular to the z-axis :
Eq 34-3![]()
![]()
At the seabed these stresses are denoted ![]() and
and ![]() .
.
For simplicity we will consider flow in the x-direction that is steady (![]() ) and uniform (
) and uniform (![]() ) so henceforth we denote
) so henceforth we denote ![]() as
as ![]() and the stress at the boundary
and the stress at the boundary ![]() as
as ![]() .
.
Consider the case of laminar flow (no turbulence) between a fixed surface and a plate of area A, separated by a height h, and moving at a steady velocity u (such that the applied force is opposed equally by the drag of the solid surface).
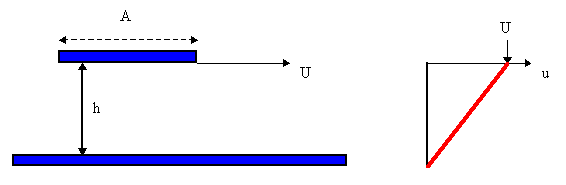
Figure 34-5
Eq 34-4:![]()
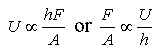
For laminar flow (of a Newtonian fluid, see below), the velocity profile would be linear:
Eq 34-5:![]()
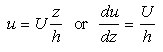
The gradient of velocity which appears in this equation is called the shear. Since the stress is the force per unit area, we use Eq 34-4 and 34-5 to write:
Eq 34-6:![]()
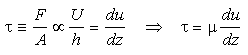
The proportionality constant µ is the absolute viscosity and is a
measure of the resistance to deformation of a fluid.
Dimensionally the stress has units of force per unit area
(g cm/s![]() )/(cm
)/(cm![]() )
and the velocity gradient units of (s
)
and the velocity gradient units of (s![]() ) so the viscosity has
units of g/(cm s). One g/(cm s) is one poise.
In seawater the viscosity depends on temperature and salinity:
) so the viscosity has
units of g/(cm s). One g/(cm s) is one poise.
In seawater the viscosity depends on temperature and salinity:
|
|
Fresh Water |
Seawater, S=35 o/oo |
||||
|
Temperature |
Density |
Absolute Viscosity |
Kinematic Viscosity |
Density |
Absolute Viscosity |
Kinematic Viscosity |
|
° C |
g/cm3 |
centipoise |
cm2/s (x 10-2) |
g/cm3 |
centipoise |
cm2/s (x 10-2) |
|
0 |
1.0000 |
1.52 |
1.52 |
1.028 |
1.61 |
1.57 |
|
10 |
.9997 |
1.31 |
1.31 |
1.027 |
1.39 |
1.35 |
|
15 |
.9991 |
1.14 |
1.14 |
1.026 |
1.22 |
1.19 |
|
20 |
.9982 |
1.005 |
1.00 |
1.025 |
1.07 |
1.05 |
|
30 |
.9956 |
0.801 |
0.804 |
1.022 |
0.87 |
0.85 |
An alternative way of thinking about the stress due to shear is as a transfer of momentum in a direction perpendicular to the surface on which the stress is acting. Multiplying the numerator and denominator by r :
Eq 34-7![]()
![]()
The stress is the product of the gradient of fluid momentum and a constant n, the kinematic viscosity.
The discussion to this point pertains to a laminar flow and is for a Newtonian fluid. We say a fluid is Newtonian when the viscosity as defined by the proportionality in Eq 34-6 is a constant.
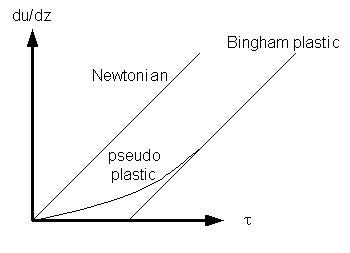
Figure 34-6
| Oceanography 540 Pages Pages Maintained by Russ McDuff (mcduff@ocean.washington.edu) Copyright (©) 1994-2001 Russell E. McDuff and G. Ross Heath; Copyright Notice Content Last Modified 1/2/2001 | Page Last Built 1/2/2001 |