At the boundary, fluid velocity slows to zero. By transport of momentum, velocity in the interior must match this condition through some adjustment mechanism that will determine the thickness of the boundary layer. Typically friction is thought to be the adjustment mechanism. Recalling that the viscous stress is:
Eq 1![]()
![]()
We can divide both sides by the density to yield:
Eq 2![]()
![]()
The dimensions of the left hand side are
Eq 3![]()
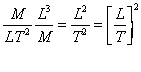
or units of velocity squared. We define a term called the friction velocity or shear velocity:
Eq 4![]()
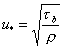
Thus
Eq 5![]()
![]()
Integrating
Eq 6![]()
![]()
Since u=0 at z=0, C=0 and:
Eq 7![]()
![]()
A record of velocity as a function of time can be characterized as fluctuations about some mean value:
Eq 8![]()
![]()
Turbulence will give rise to velocity fluctuations in both the horizontal (velocity u) and vertical (velocity w) directions characterized by u' and w'.
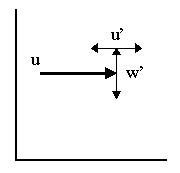
Eq 9![]()
![]()
Thus the friction velocity can be written:
Eq 10![]()
![]()
Prandtl hypothesized that turbulent fluctuations should act over some correlation scale l so that
Eq 11![]()
![]()
Thus
Eq 12![]()
![]()
von Karman further hypothesized that the correlation scale should be proportional to the distance from the boundary:
Eq 13![]()
![]()
where kappa is von Karman's constant, the turbulent momentum exchange coefficient. By experiment kappa has been found to be 0.41.
Eq 14![]()
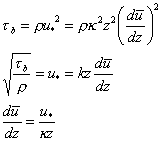
Integrating:
Eq 15![]()
![]()
Let u be 0 at z=z0. Then
Eq 16![]()
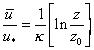
This is the von Karman-Prandtl equation, the Law of the Wall.
We can now develop the structure of the boundary layer. Very near to the boundary where viscous forces dominate there may be a viscous sub-layer where equation 1 applies. Whether this viscous sub-layer exists depends on whether the boundary is smooth or rough. If it is rough it will generate turbulence at the boundary so that turbulent forces become more important than viscous forces.
The roughness is characterized by a dimensionless number
Eq 17![]()
![]()
where ks is a length scale of the roughness elements (which may be due to grain roughness of the surface, ripple patterns, or fluid stratification)
When R* is less than 5, the flow is said to be hydrodynamically smooth (HSF), when R* is greater than 70 the flow is said to be hydrodynamically rough (HRF), when between 5 and 70 the flow is transitional.
The value of z0 for HSF and HRF have been established by experiment. For HSF:
Eq 18![]()
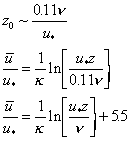
For HRF:
Eq 19![]()
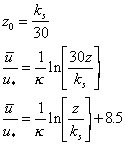
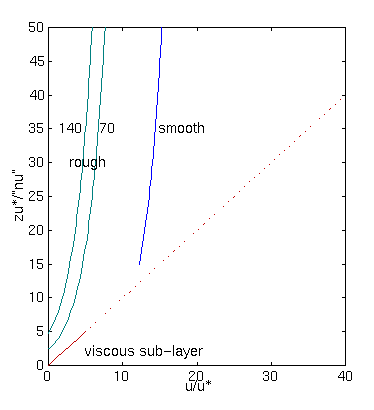
The most common way in which u* and z0 are measured is by determing the velocity profile above a boundary. The profile is fit to the Law of the Wall and the parameters from the fit used to decide whether the flow is HSF or HRF.
Eq 20![]()
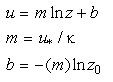
| Oceanography 540 Pages Pages Maintained by Russ McDuff (mcduff@ocean.washington.edu) Copyright (©) 1994-2001 Russell E. McDuff and G. Ross Heath; Copyright Notice Content Last Modified 2/26/2001 | Page Last Built 2/26/2001 |