Threshold of Motion

Grains forming the boundary between a fluid and a sediment possess a finite weight and finite coefficient of friction. When the applied shear stress is low they are not brought into motion. As applied shear stress is increased, a critical shear stress is reached at which grains will begin to move. The value of the critical stress will depend primarily on the size and density of the particles and secondarily on their shape and packing and the cohesive forces acting between particles.

One the critical stress is just exceeded, particles will advance in the direction of flow due to irregular jumps or less commonly rolls. This mode of tranport is termed the bedload and conceptually can be thought of as being deterministic, that is the behavior of a particle once in motion is dominanted by the gravity force. As the stress is further increased, particles will also begin to be suspended in solution and subject to turbulent forces. This mode of transport is termed the suspended load. Due to these two modes of transport there will be a flux of material across a plane perpendicular to the flow. Our ultimate goal is to determine this mass flux by integrating the product of the velocity profile and concentration profile.

The Critical Stress

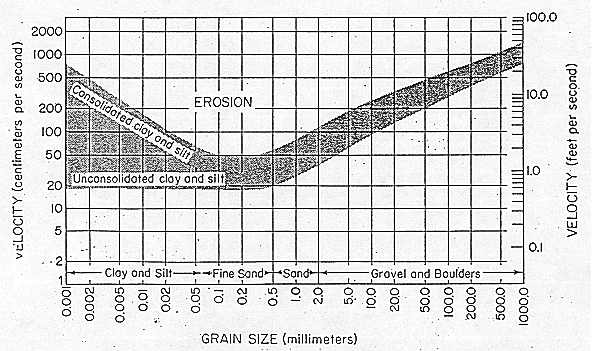
The motion of sediment can be parameterized in a number of ways. The oldest of these is due to Hjulstrom who summarized observational data in terms of fluid velocity and grain size:

Figure 36-1

There are a number of variants of the Hjulstrom diagram, using grain diameter as one parameter and some measure of the stress as the other (via the quadratic stress law: u, u100 or stress itself: ustar):

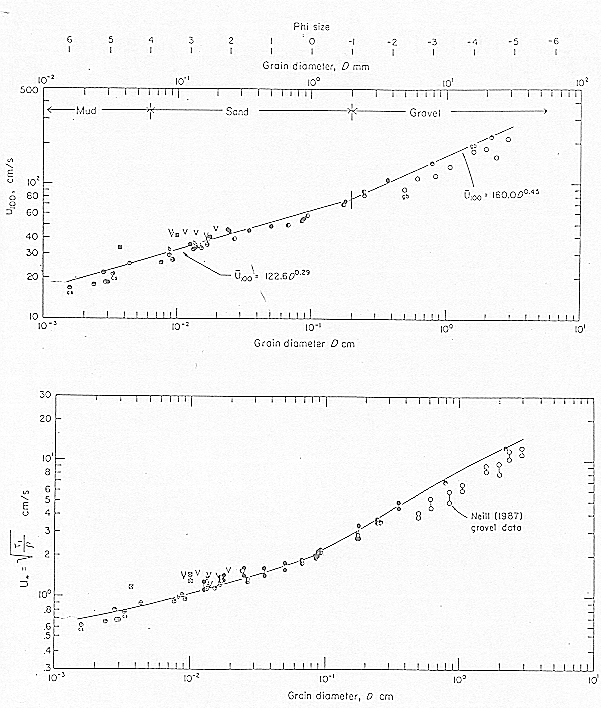
Figure 36-2

In several of these figures there is a envelope of values for small particles, contrasting unconsolidated and consolidated/cohesive sediment. This reflects the importance of interparticle forces because of the higher ratio of surface area to volume.

Shields first suggested a more general scaling, based on an analysis of the forces acting on particles. His analysis suggested an organization of the data based on two factors.

• The first is the entrainment factor, , which scales the boundary stress to the density contrast between the particles and the fluid, -, and the particle size, D and thus compares the applied stress to the gravitational force acting on an individual particle:

  Eq 36-2:

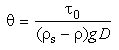
  g is the gravitational acceleration.

• The other is a Reynolds number, relevant to an individual particle, comparing turbulent and viscous forces:

  Eq 36-3:

For non-cohesive sediments, under a wide range of experimental conditions, a boundary is found in this parameter space (entrainment factor, Reynolds number) between no motion of the sediment and active erosion of the sediment:

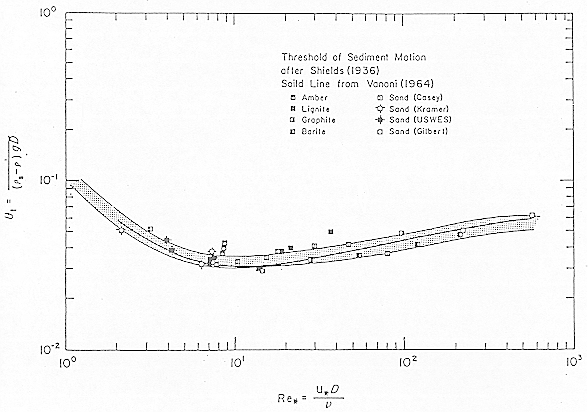
Figure 36-3

As an example consider the situation for Re=10 where (reading from Figure 36-3) the critical is 3 x 10:

Eq 36-4:

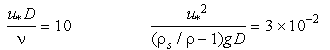
Solving each of the two equations for D:

Eq 36-5:

Equating these expressions for D:

Eq 36-6:

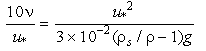
and solving for u*, we find:

Eq 36-7:

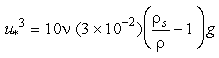
For grains of density 2.7 g/cm in water of viscosity 10 g cms (1 cp):

Eq 36-8:

That is 1.6 cm/s is the scale of the rms velocity fluctuations necessary to just begin to transport a 0.6 mm grain.