A boundary layer exhibits a velocity profile connecting a background oceanographic flow and a no-slip, zero velocity condition at a solid boundary. Schematically
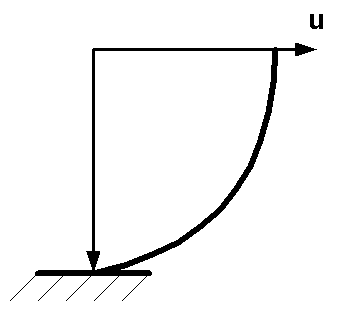
Figure 1
As we will see this gradient of velicty gives rise to transfer of momentum toward the boundary; when it is sufficient (i.e., exceeds a critical value), it can cause transport of sediment.
Shear Stress
Stress, denoted t, is a force applied to a plane surface per unit area. Dimensionally:
Eq 1![]()
![]()
Consider a volume element. Each of the three surfaces can have three forces acting on it, so there are nine components in all. They are denoted ![]() where the i subscript describes the surface (e.g., z would indicate the surface perpendicular to the z-axis) and the j subscript describes the direction of the force (e.g., x would indicate the force acting in the direction of the x-axis).
where the i subscript describes the surface (e.g., z would indicate the surface perpendicular to the z-axis) and the j subscript describes the direction of the force (e.g., x would indicate the force acting in the direction of the x-axis).
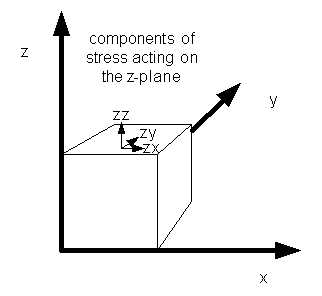
Figure 2
Eq 2![]()
![]()
Of the remaining six components, we are interested in the two acting in the x and y directions on the plane perpendicular to the z-axis :
Eq 3![]()
![]()
At the seabed these stresses are denoted ![]() and
and ![]() .
.
For simplicity we will consider flow in the x-direction that is steady (![]() ) and uniform (
) and uniform (![]() ) so henceforth we denote
) so henceforth we denote ![]() as
as ![]() and the stress at the boundary
and the stress at the boundary ![]() as
as ![]() .
.
Consider the case of laminar flow (no turbulence) between a fixed surface and a plate of area A, separated by a height h, and moving at a steady velocity u (such that the applied force is opposed equally by the drag of the solid surface).
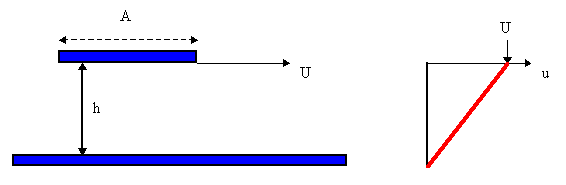
Figure 3
Eq 4:![]()
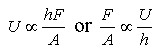
For laminar flow (of a Newtonian fluid, see below), the velocity profile would be linear:
Eq 5:![]()
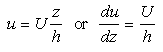
The gradient of velocity which appears in this equation is called the shear. Since the stress is the force per unit area, we use Eq 4 and 5 to write:
Eq 6:![]()
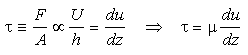
The proportionality constant µ is the absolute viscosity and is a measure of the resistance to deformation of a fluid. Dimensionally the stress has units of force per unit area (kg m/s2)/(m2) and the velocity gradient units of (s-1) so the viscosity has units of kg/(m s). [The historical cgs unit of viscotiy is the poise: 1 g/(cm s). 1 poise = 10-1 kg/(m s). In seawater the viscosity depends on temperature and salinity:
|
|
Fresh Water |
Seawater, S=35 o/oo |
||||
|
Temperature |
Density |
Absolute Viscosity |
Kinematic Viscosity |
Density |
Absolute Viscosity |
Kinematic Viscosity |
|
°C |
kg/m3 |
x 10-3 |
x 10-6 m2/s |
kg/m3 |
x 10-3 |
x 10-6 m2/s |
|
0 |
1000 |
1.52 |
1.52 |
1028 |
1.61 |
1.57 |
|
10 |
999.7 |
1.31 |
1.31 |
1027 |
1.39 |
1.35 |
|
15 |
999.1 |
1.14 |
1.14 |
1026 |
1.22 |
1.19 |
|
20 |
998.2 |
1.005 |
1.00 |
1025 |
1.07 |
1.05 |
|
30 |
995.6 |
0.801 |
0.804 |
1022 |
0.87 |
0.85 |
An alternative way of thinking about the stress due to shear is as a transfer of momentum in a direction perpendicular to the surface on which the stress is acting. Multiplying the numerator and denominator by r :
Eq 7![]()
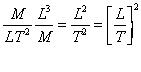
In this form the stress is seen to be the product of the vertical gradient of fluid momentum in the horizontal direction and a constant n, the kinematic viscosity.
The discussion to this point pertains to a laminar flow and is for a Newtonian fluid. We say a fluid is Newtonian when the viscosity as defined by the proportionality in Eq 6 is a constant.
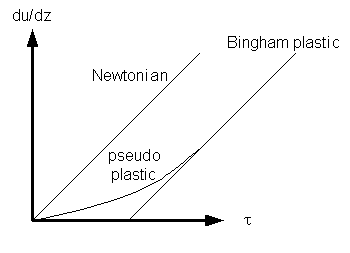
Figure 6
At the boundary, fluid velocity slows to zero. By transport of momentum, velocity in the interior must match this condition through some adjustment mechanism that will determine the thickness of the boundary layer. Typically friction is thought to be the adjustment mechanism. Recalling that the viscous stress is:
Eq 8![]()
![]()
We can divide both sides by the density to yield:
Eq 9![]()
![]()
The dimensions of the left hand side are
Eq 10![]()
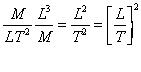
or units of velocity squared. We define a term called the friction velocity or shear velocity:
Eq 11![]()
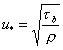
Thus
Eq 12![]()
![]()
Integrating
Eq 13![]()
![]()
Since u=0 at z=0, C=0 and:
Eq 14![]()
![]()
A record of velocity as a function of time can be characterized as fluctuations about some mean value:
Eq 15![]()
![]()
Turbulence will give rise to velocity fluctuations in both the horizontal (velocity u) and vertical (velocity w) directions characterized by u' and w'.
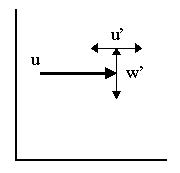
Eq 16![]()
![]()
Thus the friction velocity can be written:
Eq 17![]()
![]()
Prandtl hypothesized that turbulent fluctuations should act over some correlation scale l so that
Eq 18![]()
![]()
Thus
Eq 19![]()
![]()
von Karman further hypothesized that the correlation scale should be proportional to the distance from the boundary:
Eq 20![]()
![]()
where kappa is von Karman's constant, the turbulent momentum exchange coefficient. By experiment kappa has been found to be 0.41.
Eqs 21![]()
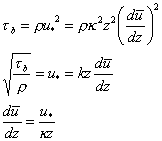
Integrating:
Eq 22![]()
![]()
Let u be 0 at z=z0. Then
Eq 23![]()
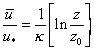
This is the von Karman-Prandtl equation, the Law of the Wall.
We can now develop the structure of the boundary layer. Very near to the boundary where viscous forces dominate there may be a viscous sub-layer where equation 1 applies. Whether this viscous sub-layer exists depends on whether the boundary is smooth or rough. If it is rough it will generate turbulence at the boundary so that turbulent forces become more important than viscous forces.
The roughness is characterized by a dimensionless number
Eq 24![]()
![]()
where ks is a length scale of the roughness elements (which may be due to grain roughness of the surface, ripple patterns, or fluid stratification)
When R* is less than 5, the flow is said to be hydrodynamically smooth (HSF), when R* is greater than 70 the flow is said to be hydrodynamically rough (HRF), when between 5 and 70 the flow is transitional.
The value of z0 for HSF and HRF have been established by experiment. For HSF:
Eq 25![]()
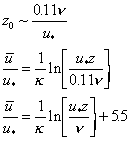
For HRF:
Eq 26![]()
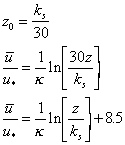
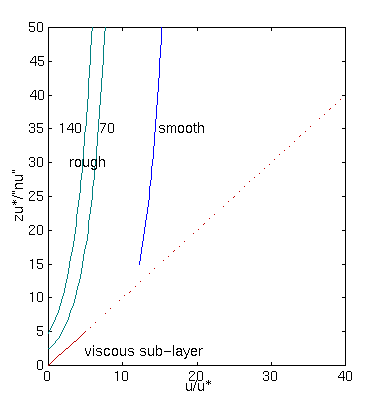
The most common way in which u* and z0 are measured is by determing the velocity profile above a boundary. The profile is fit to the Law of the Wall and the parameters from the fit used to decide whether the flow is HSF or HRF.
Eq 27![]()
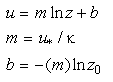
| Oceanography 540 Pages Pages Maintained by Russ McDuff (mcduff@ocean.washington.edu) Copyright (©) 1994-2002 Russell E. McDuff and G. Ross Heath; Copyright Notice Content Last Modified 12/6/2002 | Page Last Built 12/6/2002 |