Hydrothermal Fluxes

Type Examples

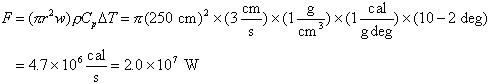
Figure 12-1. Low Temperature (~10°C) on the Galapagos Rift

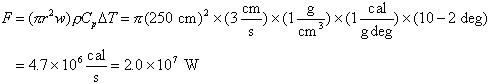
Two years later, the first black smoker vents were discovered on the East Pacific Rise at 21°N.

Figure 12-2. High Temperature (~350°C) on the East Pacific Rise at 21°N.

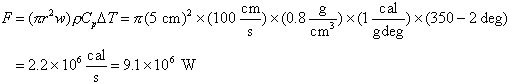
It is not surprising that these fluxes of heat are similar. Chemically the warm springs at Galapagos resemble the high temperature fluids from EPR 21N mixed with seawater. This is thought to occur in the fractured and fissured upper extrusive basalts. A Galapagos warm spring can be thought of as being fed at depth in a manner similar to the EPR hot spring.

We earlier estimated the global convective heat loss in the axial circulation cell to be 2.5 x 10¹⁹ cal/y which is 3.3 x 10¹² W. Spread over the 70,000 km of ridge this translates to 4.7 x 10⁷ W/km. Thus the heat flux from a single black smoker or warm spring is sufficient to remove the required heat from a significant portion of the mid-ocean ridge and individual vents should be relatively sparsely distributed.

However we know of major vent fields that are significantly larger. The best studied of these are on the Endeavour Segment of the Juan de Fuca Ridge, but there are also examples found at the TAG field on the Mid-Atlantic Ridge and on the Explorer Ridge. Such examples, with heat fluxes greatly exceeding the long-term geological average, provide the greatest challenge for explaining their heat source.

In terms of heat flux, the Endeavour Segment is the best studied of the examples. The Endeavour Segment is the northernmost portion of the Juan de Fuca Ridge. Four major vent fields are known separated by 2-3 km, from the south these are Mothra, Main Endeavour Field, High Rise, and Salty Dawg. Of these MEF was discovered first (1984) and has had the most scientific attention. The geology has been well mapped:

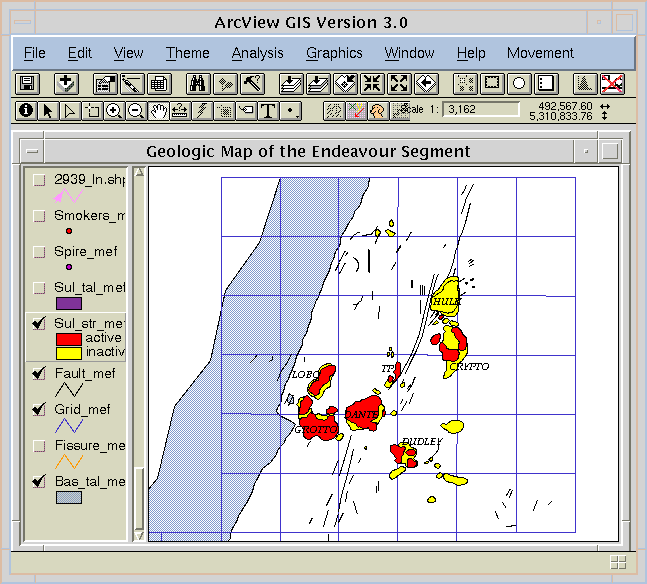
Figure 12-3 GIS rendering of the northern portion of Main Endeavour Field, Juan de Fuca Ridge. Data from the Endeavour Segment GIS Pages

Figure 12-4 CCD image of the "Dudley" sulfide structure in Main Endeavour Vent Field. The "person" in the scene is a plywood mannequin 5'6" (1.67 m) in height. Figure courtesy of Milton Smith and John R. Delaney 1991

black smoker abundance x individual contribution

3.8 x 108 W

But venting through black smokers is not the only mode of discharge from the field. There are a few small areas of warm vents similar in character to Galapagos warm vents, but in addition there is slow flow through the surfaces of the major sulfide edifices. This flow is difficult to measure, but the one determination extrapolated to the total area of sulfide surface in the field yields a much higher flux, ~10¹⁰ W.

black smoker abundance x individual contribution	3.8 x 108 W
diffuse flow from sulfide surfaces	~1010W

For a vent field of the size and complexity of MEF it is difficult to obtain a statistical meaningful estimate by direct measurement of all individual sources. An alternative is to assay the excess heat present in the water column, i.e., determine the flux of heat carried in the overlying water column plumes.

Deep-sea hydrothermal plumes are an example of turbulent, buoyant jets and plumes, a topic spanning basic physics, engineering applications and environmental phenomena. Jets and plumes are distinguished by the relative roles of momentum and buoyancy with a pure jet being momentum dominated and a pure plume being buoyancy driven. Black smoker vents are near to the jet-plume transition and rapidly develop a plume like character.

A simple model, the Morton-Taylor-Turner model, describes the essential features of plume behavior in the deep sea. This model involves conservation of mass, momentum and as many additional parameters as are necessary to describe the density contrast between the plume and the surrounding environment. The key assumption of the model is the "entrainment assumption" which establishes a proportionality between the horizontal velocity of fluid entrained from the surroundings and the vertical velocity in the core of the plume at that same level. Specifically the volume entrained is equal to

EA^1/2W

where A is the cross sectional area of the plume, W is the vertical velocity in the core of the plume and E is the entrainment coefficient. The value of E determined by extensive experiment over a wide variety of fluids and velocities is ~0.25.

With this assumption the conservation equations for mass, salt, heat and momentum are:

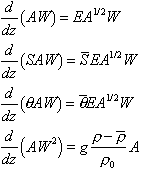
In these equations z is the vertical coordinate, S is salinity, theta is potential temperature and the bar notation denotes the variation of the property within the surrounding ambient water column. This set of equations can be integrated numberically once the properties of the venting source, an equation of state, and the local stratification are specified.

Changes in momentum are brought about by the buoyancy force acting on the fluid. Near to the source both the momentum flux M=AW² and buoyancy flux B=g (rho-rhobar)/rho AW are positive. With entrainment, the buoyancy flux decreases whiles the momentum continues to increase. At the point of zero buoyancy, the momentum reaches a maximum. Because of the ramining momentum at this level the plume overshoots. When the lvel of zero momentum is reached, the plume overturns, sinks back to its level of neutral buoyancy, and spreads laterally.

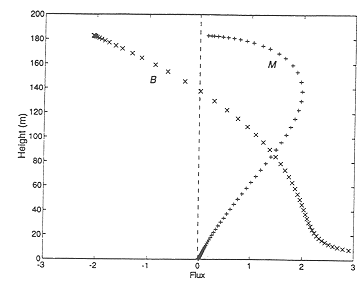
Some representative model calculations for stratfication typical of the Pacific Ocean is shown in this figure:

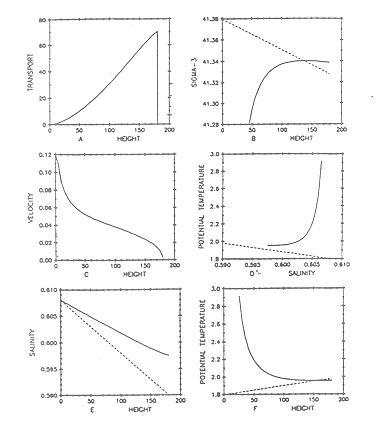
Figure 12-5. Model calculations of plume characteristics for background hydrography characteristic of the Pacific Ocean. From (45)

Hydrographic surveys show that the horizontal scale of the spreading plume is ~1 km and the thickness of the spreading layer is ~200 meters. If the net flow of water at the level of lateral spreading is determined then the heat flux can be calculated:

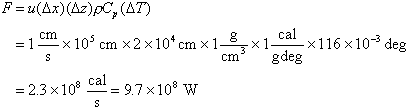
The problem with this approach is that the net transport is a long term average of tidally-dominated currents with peak velocities of order 10 cm/s. This leads to large formal uncertainties in the computed transport. For example one study reports a net transport of 1±0.8 cm/s so that the computed heat flux would be within the range 2-20 x 10⁸W.

black smoker abundance x individual contribution	3.8 x 108 W
diffuse flow from sulfide surfaces	~1010W
plume anomaly and physical transport	2-20 x 108W

A final way of estimating the heat flux is to use a radioisotopic tracer with a suitable decay time. 222-Rn is suitable for the purpose, being greatly enriched in vent fluids (for decay of 226-Ra in the crust) and with a half life of 3.8 days. The flux of Rn from the source must be balanced by decay in the water column:

Using this approach to find the transport, one calculates a heat flux of 3±2 x 10⁹W.

black smoker abundance x individual contribution	3.8 x 108 W
diffuse flow from sulfide surfaces	~1010W
plume anomaly and physical transport	2-20 x 108W
plume anomaly and Rn-based transport	3±2 x 109W