CONTROL OF CARBONATE PRESERVATION

1. Review of the Seawater Carbonate System

Carbon dioxide is present in the atmosphere:

Eq C-1:

Carbon dioxide is soluble in water:

Eq C-2:

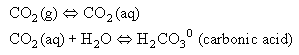
Because water is present in excess, we generally do not distinguish between these two forms, and define:

Eq C-3:

At equilibrium:

Eq C-4:

Carbonic acid is a weak diprotic acid:

Eq C-5:

Eq C-6:

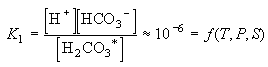
Eq C-7:

Eq C-8:

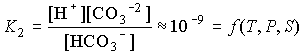
The equilibrium constants are defined for seawater medium and are functions of temperature, pressure and salinity. For completeness, water also acts as an acid:

Eq C-9:

Eq C-10:

We have 3 equations with 5 unknowns, therefore to solve the system of equations we need to specify two more conditions. One is mass conservation:

Eq C-11:

The other is a parameter called alkalinity, Alk:

Eq C-12:

The alkalinity is essentially a restatement of electroneutrality. Consider a system composed of NaCl and NaHCO₃ dissolved in water:

Eq C-13:

Correcting for the portion of the sodium with its origin in NaCl:

Eq C-14:

yields an equation analogous to the one defining the alkalinity. In general the left hand side is the sum of positive charge from cations of strong bases (e.g., NaOH) less the negative charge from anions of strong acids (e.g., HCl). C_T and Alk are measurable quantities. If they are known then the system is completely defined.

These two parameters vary systematically in the ocean:

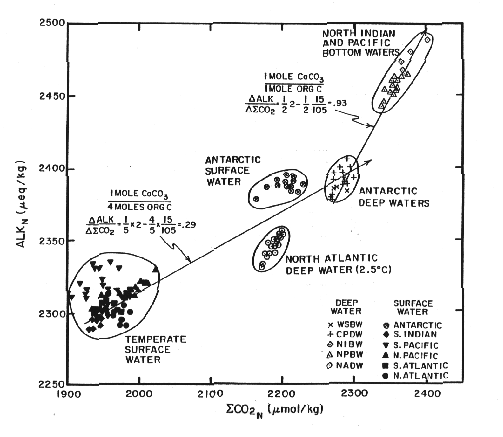
Figure C-1, from (20)

Why does it have this shape? It reflects the stoichiometry of three important processes. These are

• gas exchange:

  Eq C-15:

   

• photosynthesis-respiration:

  Eq C-16:

• carbonate precipitation-dissolution:

  Eq C-17:

Our particular interest here is in the interaction of seawater with solid CaCO₃ (s). There are two crystalline forms of calcium carbonate, calcite and aragonite. Calcite is the more stable and more common of the two. Thermodynamically:

Eq C-18:

Eq C-19:

In the ocean, the calcium/chloride ratio is constant (within 1%) so it is useful to introduce an effective constant:

Eq C-20:

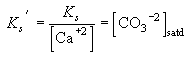
To establish where calcium carbonate is stable, we need to compare this value of the carbonate ion concentration at thermodynamic equilibrium (which will be a function of temperature, pressure and salinity) with the distribution of carbonate ion in the ocean. Consider this profile from the southern Atlantic:

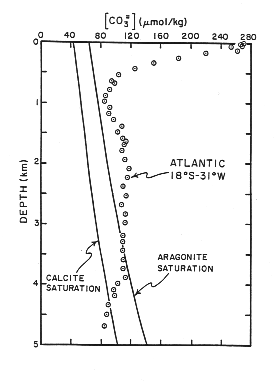
Figure C-2, from (20). Gridded data files of carbonate ion distribution, and the difference between the observed distribution and calcite solubility are available along with information on how they were constructed from David Archer, University of Chicago.

The surface waters are supersaturated and the deep waters understaturated. Aragonite becomes undersaturated at a shallower level than calcite, i.e., calcite is the stable phase at these temperatures and pressures. The oceanic distributions of carbonate ion concentration can be represented relative to the value at saturation at that same temperature and pressure:

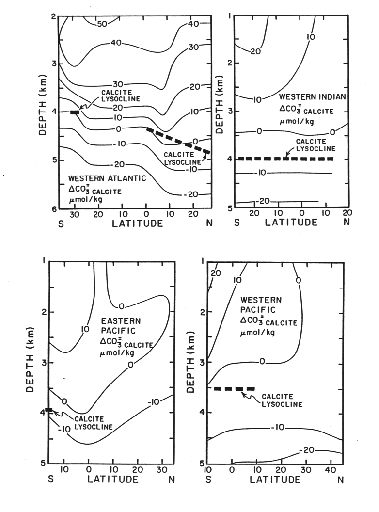
Figure C-3, from (20)

How would this saturation state be recorded in the adjacent sediment? The answer is not as simple as equating the saturation horizon with the boundary between carbonate and non-carbonate bearing sediments. Rather an important issue is the rate of supply of carbonate to the seafloor versus its rate of dissolution:

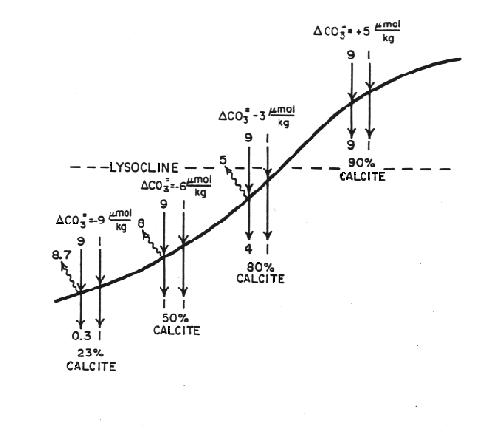
Figure C-4, from (20)

Thus two boundaries exist that can be recognized in the sediment:

• the level of the onset of dissolution or lysocline (operationally defined as the depth at which solution-resistant forams become dominant in sea floor sediments)
  
• the level of "complete" dissolution or calcite compensation depth (CCD).

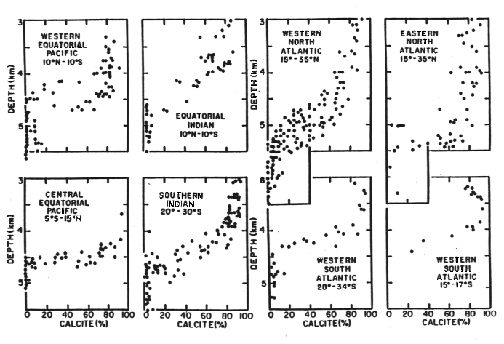
Figure C-5, from (20)

We next consider the processes controlling the position of these two horizons.

2. Dissolution of Calcium Carbonate at the Seafloor

Emerson and Bender (22) have modeled the processes involved in controlling carbonate dissolution in the sediments just below the sediment water interface. As a basis for their model we will first consider the transport equations for solutes in pore fluids.

The governing differential equation for the Emerson and Bender model has the form:

Eq C-21:

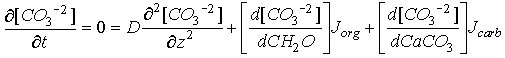
The three terms on the right hand side are respectively:

• diffusion of carbonate ion
• the effect on carbonate ion of the production of CO₂ by degradation of sedimented organic carbon
• the effect on carbonate ion of dissolution of solid CaCO₃

We first need to find the coefficients in the last two terms relating the change in carbonate ion concentration to the amount of respiration and of dissolution, respectively. The situation can be summarized by examining a plot of contours of carbonate ion concentration drawn as a function of Alk and C_T:

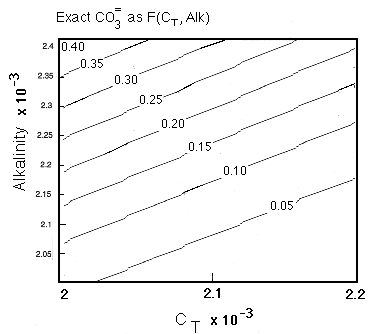
Figure C-6

In the upper left hand corner of this plot a one-to-one correspondence of the carbonate ion concentration with Alk-C_T is evident:

Eq C-22:

which is expected at pH > 7.5 when carbonate ion is dominant, but as the lower right hand corner of the figure is reached, the pH approaches 7.5 and the carbonic acid term begins to make a measureable contribution. As degradation of organic material occurs, the solution composition follows a horizontal vector to the right. Depending on where one is in the diagram, the change in carbonate ion concentration for a unit change in total carbon varies. In particular the slope is rapidly changing as one approaches the Alk=C_T line, i.e., the contours are spreading so there is less change in [CO₃^-2 ] for a given change in C_T or Alk as the solution composition approaches Alk=C_T. Because the slope we are interested in is changing rapidly in the region of interest to us, we take an alternative approach. Expressing the equilibrium as:

Eq C-23:

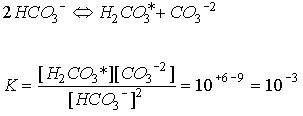
Between pH 6 and 9 the dominant form of inorganic carbon is bicarbonate and so we approximate:

Eq C-24:

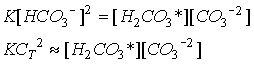
Combining equations 22-22 and 22-24:

Eq C-25:

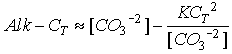
We can solve this quadratic to find a relationship between [CO₃^-2 ] and Alk-C_T, a relationship that is not particularly sensitive to the value of C_T (Fig. C-7).

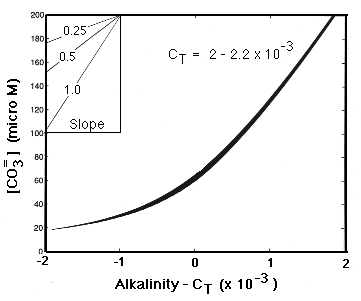
Figure C-7

At [CO₃^-2 ] = 70 micromolar (close to the saturation value at depth), the slope is about 0.5. We can then use the chain rule to relate this slope to the coefficient terms in the model:

Eq C-26:

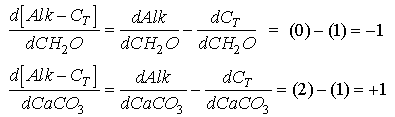
Thus

Eq C-27:

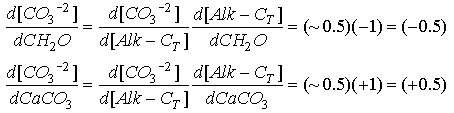
So the general model can be approximated:

Eq C-28:

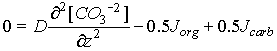
J_org and J_carb are the rates (mol/cm³/sec) of organic matter degradation and carbonate dissolution.

To describe the rate of degradation of organic matter, J_org, we postulate first order decay:

Eq C-29:

The balance between bioturbation of organic carbon associated with the solid phase (this mixing is described with an eddy diffusion coefficient K) and rate of carbon degradation is:

Eq C-30:

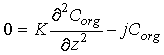
Solving this differential equation for the boundary condition: :

Eq C-31:

At steady state, the rain of organic material, R_org, has to balance degradation integrated over all depths:

Eq C-32:

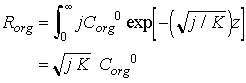
so that:

Eq C-33:

To describe the rate of calcite dissolution we adopt a first order reaction rate as a function of the saturation anomaly:

Eq C-34:

Emerson and Bender discuss the limitations of this equation in fitting data in the undersaturated part of the curve, where the rate is non-linear in the extent of undersaturation. A second limitation is whether precipitation should be allowed under supersaturated conditions.

A series of model curves (a-d) show the expected pore water profiles for sediments at various water depths (with "a" deep and below the saturation horizon and "d" shallow and above the saturation horizon):

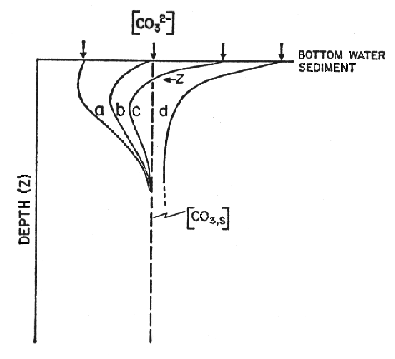
Figure C-8, from (22)

Two sets of models are considered, one with no rain of organic carbon and the other with a 1:1 ratio of rain of organic carbon and rain of calcite, a value close to that observed in deep sediment traps. The left hand panel in each figure shows the ratio of preservation to rain. The dashed curve is for the case when calcium carbonate is allowed to precipitate when supersaturated so preservation can exceed the rain rate. In the lower left, where the effect of organic carbon is included, as bioturbation is increased the effect on preservation is increased. The right hand side translates this information in the carbonate content of the sediment. When the effect of organic carbon is not included, the lysocline is at the saturation horizon and the separation between the lysocline and the CCD is about 300 meters. When the effect of organic carbon is included, the lysocline can be kilometers above the saturation horizon and the saturation horizon and the CCD are coincident.

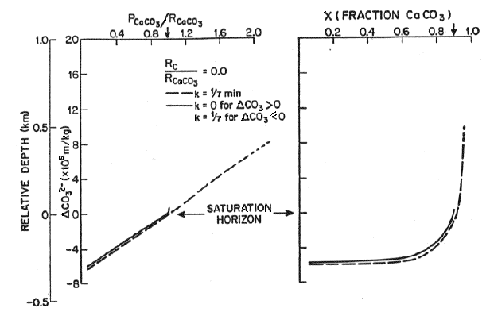
Figure C-9, from (22)

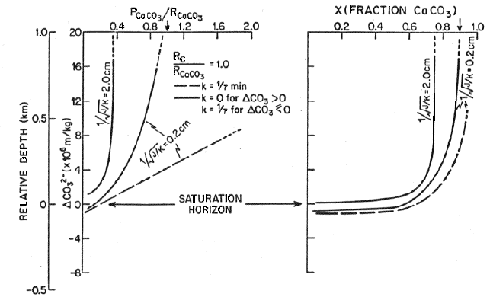
Figure C-10, from (22)

How do experimental data relate to these concepts?

Peterson, in 1966, deployed a vertical array of polished spheres made of optical grade calcite from a single mineral deposit (Figure C-11) on a mooring south of Hawaii for just over four months. The spheres were lightly etched in hydrochloric acid prior to deployment to remove any disordered layers produced by the grinding, and were weighed before and after the deployment.

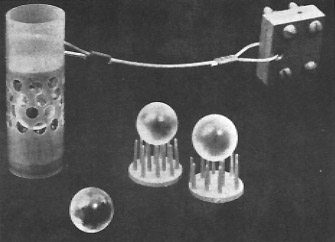
Figure C-11. Calcite spheres (about 1.5 cm diameter) used by Peterson to measure the rate of dissolution in the deep Pacific.

At a depth of about 3700 m, roughly equivalent to the lysocline, the rate of dissolution of the spheres increased rapidly and continued to increase to the sea floor (Figure C-12). The scatter in the dissolution rate from sphere to sphere was much larger than the weighing error. The source of the scatter is unknown, although it may be related to heterogeneities in the calcite or variations in the boundary layer between the spheres and circulating seawater.

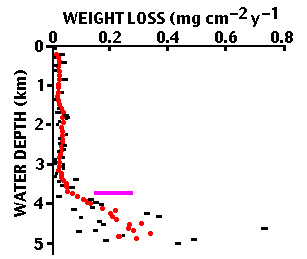
Figure C-12. Rate of dissolution of calcite spheres in the water column south of Hawaii. Circles are rates averaged over five adjacent spheres.

There have been no comparable measurements within deep-sea sediments, so the Emerson-Bender model remains untested by direct observation.

Modeling equatorial Pacific sea floor sediments.

Oxburgh (1998) has taken a different approach by using the compositions and ¹⁴C ages of equatorial Pacific sediments deposited during the last ice age and at the present sea floor to model Holocene carbonate dissolution. As shown by Figure C-13, carbonate dissolution in the bioturbated layer ("homogeneous dissolution") produces a different distribution of ¹⁴C surface sediment ages from dissolution in the water column ("non-homogeneous dissolution") or chemical erosion (mixing of old sediment up into the bioturbated layer when the dissolution rate exceeds the rain rate).

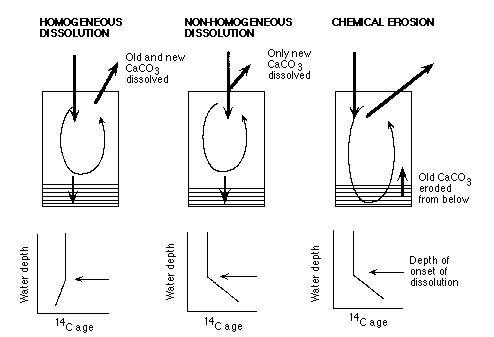
Figure C-13. Effects of different patterns of calcite dissolution on the ¹⁴C age of surface sediments as a function of water depth.

The Oxburgh model assumes an abrupt change 10,000 years ago from carbonate-rich glacial sediments (Figure C-14) to the present rain rate for carbonate measured in sediment traps from the region.

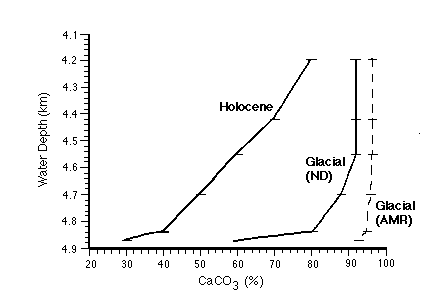
Figure C-14. Carbonate content of equatorial Pacific sediment cores as a function of water depth and age (glacial and Holocene, or postglacial). "Glacial (AMR)" assumes a pulse of rapid accumulation of carbonate at the end of the glacial as proposed by Archer and Maier-Reimer (1994).

The model assumes a mixed layer depth of 11 cm (based on ¹⁴C measurements in many cores from the region) and a non-carbonate rain rate of 0.15 +/- 0.05 g cm^-2 ky^-1. It then calculates the mass of carbonate in the mixed layer every 100 years from 10 ky to the present, using an appropriate mix of homogeneous and non-homogeneous dissolution to constrain the carbonate content to arrive at the present values (Figure C-14), and the surface sediment ¹⁴C also to match the present values (Figure C-15).

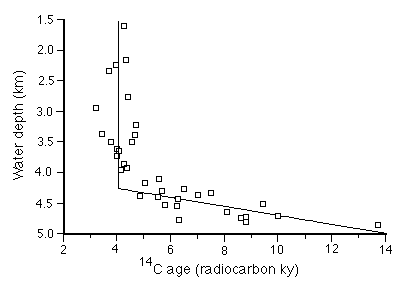
Figure C-15. Measured 14C ages of surface sediments in the equatorial Pacific.

For a carbonate rain rate of 1.85 g cm^-2 ky^-1, the time evolution of the carbonate content of the mixed layer is given by a mass conservation equation, which yields P_c:

Eq C-35:

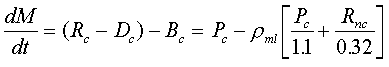
with the initial condition that

where M is the mass of carbonate in the mixed layer, P is the preservation rate, h is the bioturbation (mixed layer) depth, is density, f is the fractional carbonate content, R is the rain rate, D is the dissolution rate, B is the burial rate, and the subscript G denotes glacial, c carbonate, nc non-carbonate, and ml mixed layer.

A separate conservation equation for ¹⁴C in the mixed layer, which yields D_nh, is given by:

Eq C-36:

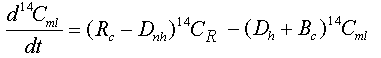
with the initial condition

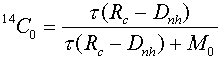
and where, in addition to the symbols above, is the mean life of ¹⁴C (8,267 years), and the subscript h denotes homogeneous, and nh non-homogeneous. The model is summarized in Figure C-16.

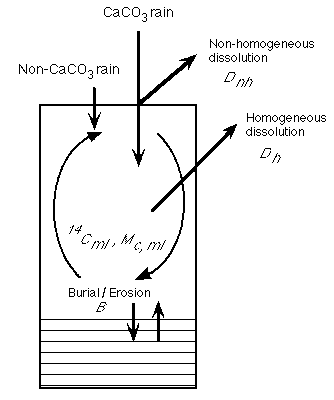
Figure C-16. Terms in the model which determine the dissolution necessary to produce the present day carbonate content and ¹⁴C surface ages as a function of age and water depth for modern equatorial Pacific sediments. See text for key to symbols.

Relative to the steady state flux required to produce the observed carbonate content and accumulation rate, all the model runs for all depths and all variations of the non-carbonate rain rate (Figure C-17) showed a preservation deficit (i.e. excess dissolution), implying that this area of the Pacific is currently not at steady state with respect to carbonate deposition for either the AMR or stepwise glacial-Holocene cases.

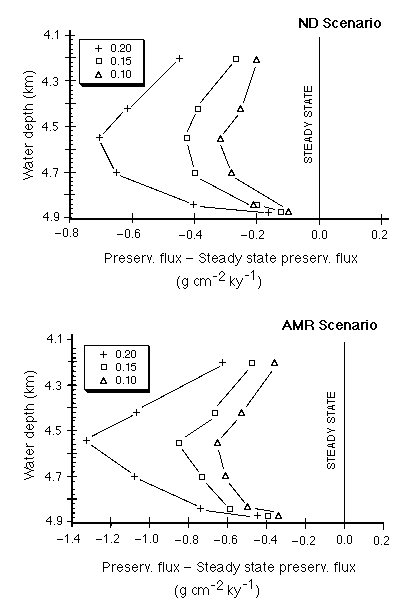
Figure C-17. Preservation flux from the Oxburgh model relative to the steady state preservation flux as a function of water depth for three non-carbonate rain rates. ND is for the observed late glacial carbonate content, AMR is for the Archer and Meier-Reimer pulse of carbonate deposition at the beginning of the Holocene. Note that all calculations yield negative carbonate fluxes relative to steady state.

Even if the carbonate rain rate is adjusted to recognize a factor-of-two decrease from the equator to 4º N, all calculated preservation fluxes below about 4,200 meters remain negative (Figure C-18), suggesting that glacial age carbonates are being actively chemically eroded at the present time. In all cases, nonhomogeneous (water column) dissolution exceeds homogeneous (mixed layer) dissolution.

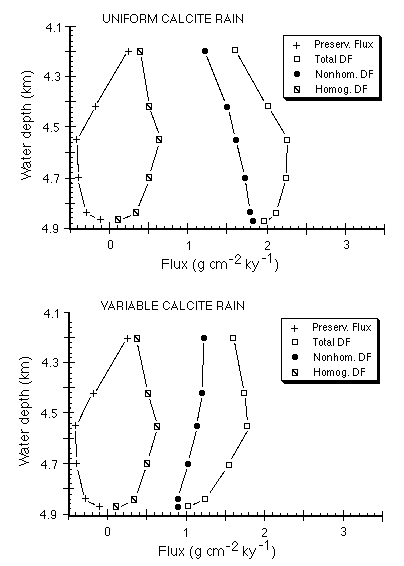
Figure C-18. Dissolution and preservation fluxes of carbonate as a function of water depth for a uniform calcite rain rate over the eastern equatorial Pacific, and assuming a 50% decrease in calcite rain rate as a function of latitude from the equator to 4º N.

The Oxburgh results lend support to the Emerson and Bender (1981) model which is otherwise difficult to reconcile with steady state deposition in the equatorial Pacific.

One other idea to bring into the discussion is the control of the level of saturation. Ignoring details of the accumulation in the zone between the lysocline and the calcite compensation depth, assume that the preservation can take two possible values

• if the seafloor is above the saturation horizon, then the preservation is equal to the rain rate
• if the seafloor is below the saturation horizon, then the preservation is zero

If we balance the river flux of calcium into the oceans with the calcium carbonate preserved in sediments:

Eq C-37:

This implies:

Eq C-38:

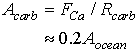
This area of carbonate sediment has to be the shallowest 20% of the ocean basin which based on this hypsometric curve would place the CCD at about 2.2 km:

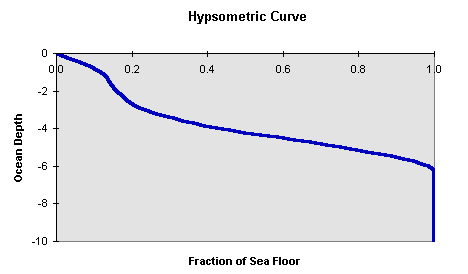
Figure C-19.

There is considerable uncertainty in the 20% figure. If calculated directly from the above equation using the range of observed rain rates, one would find values of 7-32%--the higher percentage corresponding to the the lowest rain rate. The actual distribution of sediment types indicates a number at the high end of the range. This is not unexpected--the sediment trap measurements are biased toward productive areas where the rain rate is greatest, but zones of upwelling are a relatively small portion of the waters overlying carbonate-bearing sediments.

Consider also the dependence on the river flux of calcium and the rain rate from surface waters. For constant calcium flux to ocean, the CCD shoals with increased rain rate and deepens with decreased rain rate. With constant rain rate and changing calcium flux, an increased calcium flux causes the CCD to deepen and a decreased calcium flux causes it to shoal.