Particle Collisions and Aggregation

Particle-Particle Interactions

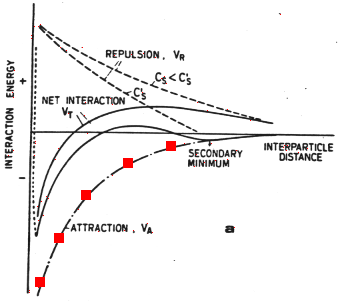
Figure 1a

At very close approach the Born repulsion of adjacent electron clouds (marked in blue) begins to play a role, so in the absence of any other forces there is a strong energy minimum with distances of approach of order 1 nm.

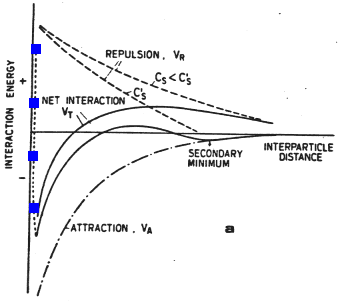
Figure 1b

There is an additional important term, the electrostatic interaction of particles. Particles in water generally have a surface charge, acquired by ionization of atoms at the surface of the particle. Surfaces exhibit acid-base behavior with surfaces becoming more negatively charged with increasing pH. This acid-base behavior leads to positive surface charge at low pH and negative surface charge at intermediate and high pH for a variety of materials. At moderate pH most surfaces are negatively charged.

The electrostatic repulsion (marked in cyan), the van der Waals attraction, and the Born repulsion combine to give the overall energy of interaction:

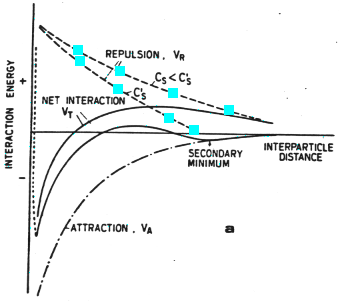
Figure 1c

As a function of ionic strength, the overall interaction undergoes a sharp transition from repulsive to attractive:

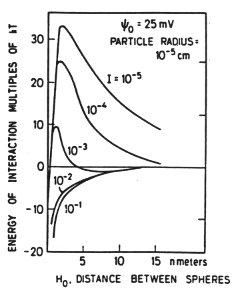
Figure 2

Particles can also adhere through specific chemical interactions. In particular coatings of biopolymers, in addition to having electrostatic interactions, can bridge between particles by forming chemical bonds with a range of energies (hydrogen bonding, covalent bonding).

Particle Collisions

Particles move simply because of their thermal energy, i.e., they undergo Brownian motion. Consider a disperse suspension of one size of particles that have some tendency to aggregate. The rate of change of the number density of particles will be described by:

Eq 1:

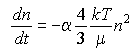
where n is the concentration of particles (particles/volume: L^-3), t is time, is the fraction of collisions leading to aggregation (=1 all adhere, =0 none adhere), T is the temperature, and µ is fluid viscosity. Thus:

Eq 2:

Eq 3:

At 25°C, the value of k_p is 5.5 x 10^-18 m³s^-1.

Suppose is one and consider as an example 1 µm particles in a 1 g/l suspension. Each particle has a mass of about 10^-14kg so the concentration of particles is about 10¹⁴m^-3. What is the time to halve the concentration of particles? Solving equation 24-5 for the initial condition n(t=0)=n:

Eq 4:

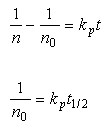
At this particle density, the characteristic time is about 30 minutes. If the particles were a factor of ten larger (10 µm), then the characteristic time would increase to about 21 days. If we compare to the Stokes settling times, we see that the effect is only important for the smallest particles.

The discussion can be made more general by introducing the mathematical concept of a coagulation kernel, a means of unifying the treatment of different physical mechanisms for particle collisions:

Eq 5:

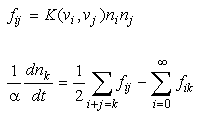
In these expressions, f is the frequency of collision of particles. The subscripts i and j denote size classes of particles of volume v. The time rate of change of particle concentration in the k size class is given by two terms. The first represents the particular combinations of smaller particles that can aggregate to form a particle exactly in size class k. The second represents the disappearance of particles from the k size class due to collision and aggregation with all size classes. The frequency of collision is the product of a coagulation kernel and the particle density in two size classes, e.g., for Brownian motion:

Eq 6:

where the kernel is given by:

Eq 7:

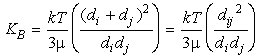
We can compare this expression to our earlier discussion of Brownian motion if we consider a monodisperse (single particle size) suspension:

Eq 8:

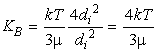
(For a monodisperse suspension there are no smaller particles from which to make particles of the initial size so that the first term in equation 24-7 is zero.)

A useful way of visualizing the magnitude of the kernel is to consider it size for a particular particle size as a function of the size of the other particle:

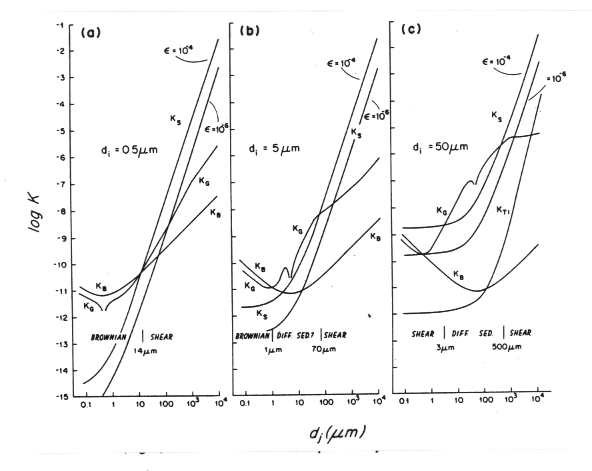
Figure 3, (35)

This figure shows (among other things) the Brownian motion kernel for three different values of d. There is a minimum at the point d=d with a 1/d dependence at smaller d and a d dependence at larger d.

Brownian motion is not the only mechanism which can bring particles together. In the presence of shear, particles at one level are traveling at a velocity different from those on another level leading to collisions.

The coagulation kernel due to shear is given by:

Eq 9:

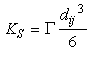
If the flow is laminar:

Eq 10:

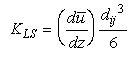
If the flow is turbulent:

Eq 11:

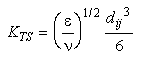
where is the turbulent dissipation rate and the kinematic viscosity.

We can compare the relative sizes of the kernels for Brownian motion and shear:

Eq 12:

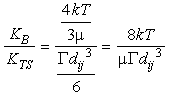
In the lower 100 m of the water column, ~0.1 s, so for a monodisperse suspension the boundary between dominance of the two mechanisms falls at a particle size given by:

Eq 13:

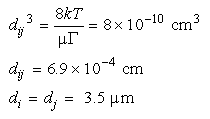
If the suspension is monodisperse, then Brownian motion is more important in bring about collisions for particles smaller than 3.5 µm and shear is more important for particles larger than 3.5 µm.

Figure 3 also shows the behavior of the kernel for collisions due to shear for two different values of the turbulent dissipation rate. When d is small, the value of the kernel approaches a constant value controlled by d: K~d/6. When d is large, the value of the kernel follows the cubic dependence on d: K~d/6.

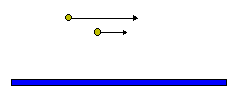
Particles also come together by differential settling with larger particles sweeping out smaller particles.

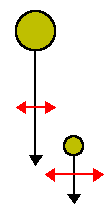
The kernel for this process is given by:

Eq 14:

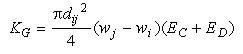
where w is the settling velocity (denoted by the black arrows), E is the collision cross-section, and E is the enhancement of the collision cross section by Brownian motion (denoted by the red arrows). E and E are complicated functions of the sizes of the particles and thus so is the kernel (Figure 3).

The relative sizes of the coagulation kernels summarized in Figure 3 indicates that different mechanisms are important for different sized particles. For very small particles, Brownian motion and shear are important mechanisms. For intermediate sized particles, all three mechanisms can play a role. For the large particles, differential settling is dominant except for interactions with much larger and smaller particles.

It is important to keep in mind that Figure 3 is somewhat misleading in that it contains no information on the particle size distribution, while the frequency of collisions depend both on the magnitude of the particle densities and the kernel. n(d) is strongly size dependent:

Figure 4, (35)

By combining the information in these two figures, we can estimate the residence time of particles in various size classes and compare these to the residence time due to Stokes settling through the lower 100 meters of the water column (these residence times are in years):

Coagulation through Brownian motion moves particles to larger size classes where they are removed by Stokes settling. Note that the residence time will have a maximum somewhere between 0.5 and 5 µm.

• shape. In order for the van der Waals attraction to be strong, the particles need to be aligned. A rough surface geometry can prevent this.
• shear. Shear at the surface of a aggregated particle can dislodge individual particles. While progress has been made in representing this process with a disaggregation kernel, the net effect is often included within an effective value for GRKalpha|.

For more information on this topic see references (35), (36) and (37).