Conduction and the Conductive Plate Model

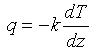
Eq 3-1:

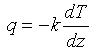
(conductive heat flux, q) = - (thermal conductivity, k) x (temperature gradient, dT/dz)

The negative sign reflects that heat is transported in the direction of lower temperature. For a historical discussion of Fourier's Law and its influence on the description of other physical systems, see (44). In dimensional terms:

Dimensions for Heat Transfer Quantities

	recent literature (SI)	older literature
flux	W m	cal cms
thermal conductivity	W mK	cal cms°C
gradient	K m	°C m

The pratical unit from older literature is the HFU (heat flow unit). 1 HFU (heat flow unit) = 41.9 mW m = 1 µcal cms The global average conductive heat flow is about 2 HFU.

The thermal conductivity (or equivalently the specific thermal conductivity, (also called the thermal diffusivity) which includes the density and heat capacity of a material) varies considerably, over about four orders of magnitude in various solid materials:

Table I. Thermal Conductivities of Common Materials

	k [W m°C]	=k/(C) [10-8 m2s-1]
	thermal conductivity	specific thermal conductivity or thermal diffusivity
air	.025	1938
water	0.6	14
ice	2.1	104
aluminum	237	9975
copper	390	11161
fiber glass	0.04	44
surficial ocean sediment	0.9	20
basaltic ocean crust	2.9	77
upper mantle	3.1	80
quartz	3	141
saturated sand	2.7	102

Using observations of the conductive heat flow we can estimate the temperature increase with depth into the oceanic lithosphere. At 100 My crustal age the heat flow is ~1.1 HFU = 46 mW m, so:

Eq 3-2:q=-k(dT/dz)

Eq 3-3:46 x 10 W m = 3.1 W m°C (dT/dz)

Eq 3-4:(dT/dz) = 15 x 10 °C m

Thus, at 100 km depth, T ~1500 °C. (This is an overestimate, as even after 100 My, the lithosphere is continuing to cool and so the profile is not strictly linear.)

This approach is reversed in order to make heat flow measurements: the temperature gradient is measured with a probe consisting of a number of thermistors which is inserted into sediment; the thermal conductivity is measured (by measuring the response after a thermal perturbation) or estimated from other data; the product yields the heat flow.

To make use of Fourier's Law to understand the rate of change of the temperature of a material, we need to establish a thermal balance for a small volume element. Again in one-dimension, we balance the fluxes of heat through the two surfaces and the internal production of heat per unit volume, H, to determine the temperature change in an interval of time dt:

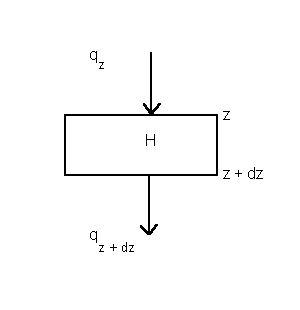
Figure 3-1

Conservation of heat requires that:

Eq 3-5:

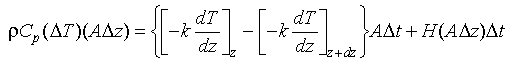
Rearranging equation 3-5 and taking to limits:

Eq 3-6:

Is Internal Production of Heat Important Within the Lithosphere?

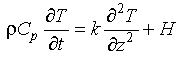
Well away from the ridge axis where the time rate of change becomes small, it becomes appropriate to consider the steady-state characteristics of equation 3-6. The goal is to examine whether the internal production of heat, H has a significant influence on the temperature distribution.

At steady state:

Eq 3-7:

Equation 3-7 is solved by integrating twice to find:

Eq 3-8:

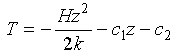
The two constants of integration are found by specifying the temperature at the sediment surface:

Eq 3-9:

and the surface heat flow

Eq 3-10:

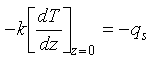
Combining equations 3-8, 3-9 and 3-10, we find:

Eq 3-11:

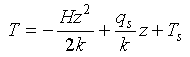
If H=0, the temperature increases linearly with depth. For positive internal production of heat, there is a negative deviation from this linear trend which grows as z squared. (The deviation is negative because of the boundary conditions we have chosen; as H increases more of the surface heat flux is derived from internal production of heat and less from the flux of heat from below). In the case of the lithosphere, is this deviation important? Because the elements U, Th and K are partitioned into the liquid as the mantle melts, considering the radiogenic production of heat in the basaltic crustal layer represents a worst case (i.e., the mantle must have a lower content of U, Th, and K). This production is 7.8x10 W m. At 6 km depth, for surface heat flow of 45 mW m and with this value of H the temperature deviation is 0.97°C from the value without internal production, 93°C. We conclude that we can generally neglect internal production of heat.

Thus for application to conductive heat loss from the lithosphere we neglect H and equation 3-6 becomes:

Eq 3-12:

Conductive Plate Model--Boundary Layer Approach

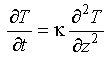
Eq 3-13:

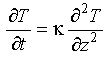
Imagine that at the axis of spreading that material is held at the temperature of melting, in other words an appropriate initial condition is that at all depths:

Eq 3-14:

(While we will not develop it explicitly, 'temperature' here means 'potential temperature'). For now also imagine that the Earth is infinitely thick, i.e., the geometry is that of an infinite half space and so at great depth:

Eq 3-15:

Finally the upper surface will be will be held at the temperature of the deep ocean:

Eq 3-16:

Omitting the details of solution, we find that:

Eq 3-17:

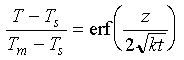
(Note the k inside the root operator should be kappa.) We can use equation 3-17 to calculate the temperature field of an evolving lithosphere.

The error function is defined by the integral:

and exhibits the behavior:

To illustrate the temperature field, we adopt T=1400 °C, the approximate temperature of the liquidus. For depth we will work in units of km, and for time in units of My so that the appropriate thermal diffusivity is 25 (km)/(My). We will build a grid for 0 to 100 km depth and 0 to 100 My of crustal age in steps of 5 km and 5 My respectively. The solution at t=0 has to be taken directly from equation 3-2 because of the singularity at t=0 in equation 3-5. The calculations are done with the MATLAB script, plate.m:

kappa=25;
Tmelt=1400;
z=0:5:100;
t=0:5:100;
for I=1:1:21
T(I,1)=Tmelt;
for J=2:1:21
T(I,J)=Tmelt*erf(z(I)/(2*sqrt(kappa*t(J))));
end
end
cs=contour(t,-z,T);
clabel(cs)

If we think of the base of the lithosphere as corresponding to a particular isotherm, say the 1200 °C isotherm which is approximately the temperature of the solidus, we can trace the growing thickness of the lithosphere as the crust ages. However, because of the semi-infinite geometry adopted, it grows to an unreasonable large thickness, as compared to the constraints provided by seismic studies of the oceanic lithosphere. The temperature gradient (and the conductive heat flux) decreases, most rapidly at first and then more slowly.

While there are some problems evident in the model: specifically

1. the temperature of the seafloor at the ridge axis is not T_m and
2. the thickness of the lithosphere does not grow without limit

Conductive Heat Flow versus Age

By taking the derivative of equation 3-17 to obtain an expression for dT/dz evaluated at z=0 and substituting into equation 3-2 we find that (details):

Eq 3-18:

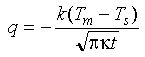
The heat flow predicted from the boundary layer model decreases with an inverse proportionality to the square root of age.

For now (we will later refine these parameters) we can estimate the relationship using a value of T of 1400 °C and the thermal conductivity data given in Table I:

Eq 3-19:

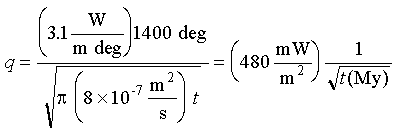
480 mW/m is ~12 HFU.

Conductive heat flow versus age, from (43)

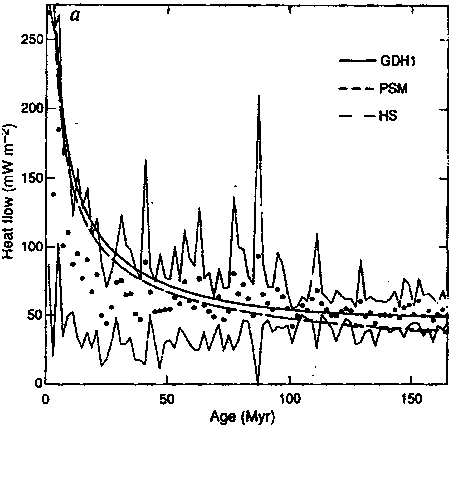
HS is our infinite half space model, PSM is the original Parsons Sclater model (8), GDH1 is the more recent Stein and Stein ((43)) fit to the global data set. (HS and PSM can only be distinguished on very old lithosphere.)